Zapotrzebowanie energetyczne to ilość energii, którą powinniśmy spożyć wraz z jedzeniem (kalorie, które jemy). Potrzebna jest ona nam do utrzymania masy ciała, aktywności fizycznej, dobrego stanu zdrowia czy występowaniu miesiączki.
Z czego składa się zapotrzebowanie energetyczne?
BMR – (PPM) podstawowa przemiana materii, czyli ilość kalorii, którą organizm potrzebuje, aby mógł funkcjonować. Potrzebujemy tyle kalorii, jakbyśmy leżeli przez cały dzień;
TEF – efekt termiczny jedzenia, czyli kalorie potrzebne na strawienie tego, co zjemy;
EAT – termogeneza wynikająca z ćwiczeń, czyli kalorie przepalane podczas treningu (zaplanowana aktywność fizyczna);
NEAT – termogeneza związana ze spontaniczną aktywnością poza treningową, czyli wszystko, co spalimy na czynności, które nie są utrzymaniem nas przy życiu, jedzeniem czy treningiem. Zalicza się do tego np. gestykulacja, wybranie schodów zamiast windy, spacer, sposób przemieszczania się, wiercenie czy utrzymanie pozycji jak siedzimy/stoimy;
EPOC – po posiłkowa konsumpcja tlenu jednak jej wartości są niewielkie;
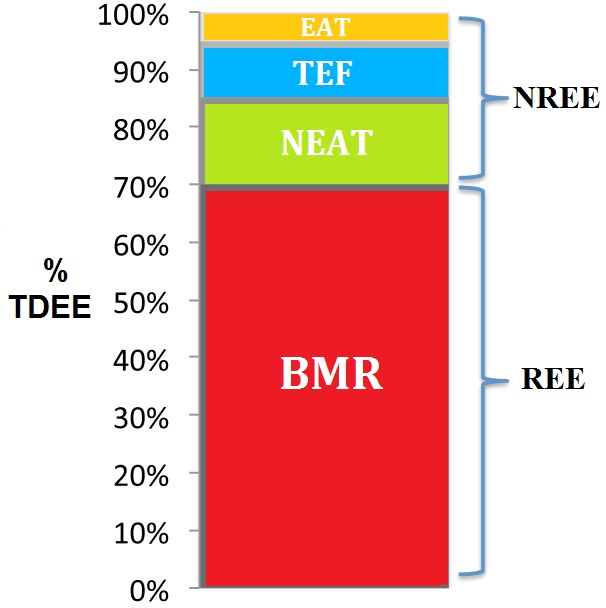
TDEE – nazywane także metabolizmem, całkowite dzienne zużycie energii;
REE – spoczynkowy wydatek energetyczny;
NREE – niespoczynkowy wydatek energetyczny
Metody obliczania podstawowej przemiany materii
Wzór Mifflina [2]:
Dla mężczyzn: BMR [kcal] = (10 ×masa ciała w kg) + (6,25 × wzrost w cm) – (5 × wiek w latach) + 5,
Dla kobiet: BMR [kcal] = (10 ×masa ciała w kg) + (6,25 × wzrost w cm) – (5 × wiek w latach) – 16.
Wzór Harrisa-Benedicta [3]:
Dla mężczyzn: BMR [kcal] = 66,47 + (13,75 × masa ciała w kg) + (5 × wysokość ciała w cm) – (6,75 × wiek),
Dla kobiet: BMR [kcal] = 665,09 + (9,56 × masa ciała w kg) + (1,85 × wysokość ciała w cm) – (4,67 × wiek).
Przykład:
Paweł, 35 lat, 185 cm, 90 kg
BMR = 66,47 + (13,75 × 90 kg) + (5 × 185 cm) – (6,75 × 35) = 1992,72 kcal
Tyle kalorii potrzebuje Paweł do zaspokojenia podstawowych funkcji życiowych, gdyby cały czas leżał.
Jak uzyskać całkowitą przemianę materii TDEE?
Wynik, który otrzymaliśmy podczas obliczenia BMR, należy pomnożyć przez współczynnik PAL. Jego wartość zależy od naszej aktywności.
1,2 – 1,39 – Brak aktywności fizycznej/osoba leżąca,
1,4 -1,69 – Niska aktywność fizyczna = siedzący tryb życia, mała ilość spacerów lub sporadyczne ćwiczenia fizyczne 1-3 razy w tygodniu bądź ich brak,
1,7 – 1,99 – Umiarkowana aktywność fizyczna – praca fizyczna/praca siedząca plus godzina treningu dziennie (np. bieganie, sport drużynowy),
2 – 2,4 – Wysoka aktywność fizyczna – ciężka praca fizyczna (np. na budowie, na polu, w kopalni) lub codzienne ciężkie treningi ok. 2 godz.,
>2,4 – Bardzo wysoka aktywność fizyczna – sportowiec zawodowy, ciężkie codzienne treningi, np. triathlon, kolarstwo na zawodowym poziomie.
Dużo osób przeszacowuje swoją aktywność fizyczną. Jeśli cały dzień siedzisz i pójdziesz 3 razy w tygodniu na siłownię, to nie masz umiarkowanej aktywności fizycznej, tylko niską i wątpię, żeby była ona w górnej granicy.
Przykład
Paweł siedzi w pracy 8 godzin, do pracy dojeżdża rowerem 5 km w jedną stronę, 3 razy w tygodniu biega przez 1 godzinę.
TDEE = 1992,72 kcal x 1,6 = 3188,35 kcal
Taką ilość energii potrzebuje Paweł, aby utrzymać masę ciała. Oczywiście nie da się za pomocą wzorów dokładnie określić ilości kalorii ze względu na duże zmienne oraz wysoki wpływ neat’u na całkowity TDEE. Temat neat’u rozwinę dokładnie w następnym wpisie. Ilość kalorii jest na pewno zbliżona, lecz trzeba obserwować, jak się zachowuje ciało.
W razie pytań lub innych spraw napisz do mnie w zakładce kontakt.
Odwiedź media społecznościowe:
♦️Instagram
♦️TikTok
♦️Facebook
Sprawdź serwer na Discord.
Bibliografia
wpDiscuz